 へ
へ
2008年2月6日
第15回.
期末試験
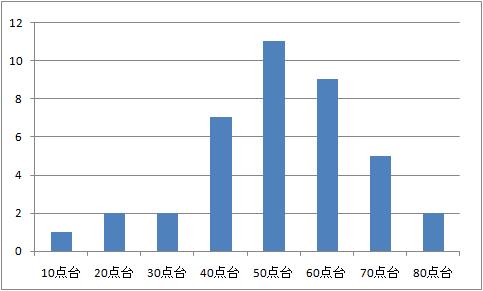
出席者39名.予想より少なかったのが残念.
2008年1月30日
第14回.
ストクスの定理の意味,ストークスの定理の証明,ストークスの定理からわかること
ストークスの定理の説明と演習.
多変数関数は何を独立変数に取っているかで微分の意味なども変わってくる.
変数を省略して書くことも多いので要注意.
ここでしっかり理解しておくこと.
教科書にあるラグランジュの未定乗数法はやる時間が取れなかったので省略しましたが,物理では条件付きで極致を探す問題に威力を発揮する一見不思議な方法です.
この本の説明はとても丁寧なので各自自習してください.
講義ノートの式番号の訂正:P.43,(4.0.7)-->(1,3,18); P.44,(4.0.7)-->(3.4.1);P.45, (4.0.7)-->(3.5.1).
今日の演習問題は添削をして土曜日の昼前から私の部屋(理611)の前に置いておきます.
試験勉強の参考にしてください.
出席者40名.
2008年1月23日
第13回.
演習問題の解説,ガウスの定理の意味とその証明
宿題にしておいた演習問題の一部を解説.
回収した演習を見ていると全く何もできていない人が数人いる.
40人以上は単位を出したいと思っているのだが難しいかもしれない.
試験は2月6日に同じ場所,同じ時間でやります.
成績は基本的には試験の結果でつけるので,出席不足,演習不出来などのひとも,本番でよくできればOKです.
出席だけでは単位は取れません.
出席者41名.
2008年1月16日
第12回.
2重積分の順序,積分変数の変換,多重積分とヤコビアン,面積分,ベクトル関数の面積分
時間が足りなくなり,演習を宿題とする羽目になった.宿題を出すことにはしたくなかったので残念.
あと2回だがストークスの定理までは確実に行ける.
どこまでを数学の講義で学んでいるのかが分からずやりにくい.
繰り返しも理解を深めるのに役立つと思ってやっているのだが、進度が遅れるだけで思惑通りの効果があるのかわからない.
講義の途中で急に静かになり緊張が高まるのを感じることがある.
きっとそこからが本当に初めて聞く新しい内容なのだろう.
出席者42名.
2007年12月19日
第11回.
線積分の意味と定義,線積分の経路,パラメタ積分,ベクトルの線積分,勾配ベクトルの線積分,2重積分
積分の話は数学で学んだことの復習が多い.できるだけさらっとその意味を復習する.
慣れないと,線積分の意味やベクトルの積分の概念は混乱しやすい.
この講義も教科書も演習問題の数は少ないので,適当な演習書をやってなじむことが大切.
出席者43名.
2007年12月12日
第10回.
2次元極座標でのベクトルの表示,2次限極座標での微分演算子,勾配,発散,ラクラシアン,完全反対称単位テンソルの使い方.
これでベクトルの微分はおしまい.来週からは積分に入る.
教科書にはこのあたりの話は書いてないので,もう少し勉強したい人はベクトル解析の入門書を探して見てください.
演習問題を見ていると,普通のベクトルの公式で最後に微分演算子に置き換えたものが多かった.
途中の演算が微分演算子でも同様に成り立つか確かめないと意味のない答えです.
出席者43名.
2007年12月05日
第9回.
レポート問題解説,超流動の渦,ラプラス演算子,2次元極座標.
演習問題を丁寧に解説した.具体例は重要なものを挙げてあるので図を描いて,ベクトル場の具体的な感じをつかんでおくとよい.
演習を見るとベクトル場の概念が混乱している人がいるのが気になる.
そういう人は教科書などを丁寧に読んで復習すること.
ここであいまいにするとすぐに完全に脱落します.
ミスプリ訂正:P.31 (4.0.1) --> (2.3.35).レポートの略解,2の後半 r3 --> r4.
出席者45名.
2007年11月28日
第8回.
発散の復習,ベクトル場の回転,回転の意味,剛体の回転,レポート演習第3回.
ラプラシアンの説明まで行かなかったが,演習レポートを実施.
最後に求めてある公式の証明はやっておくこと.
とくに一目で分からない複雑なものは計算練習にもなるので是非やってください.
出席者43名.
2007年11月21日
第7回.
空間曲線,ベクトル場とは何か,勾配,ベクトル場の発散,流体の流れと発散の意味.
また演習の時間が不足した.全部できた人は1,2名.来週詳しく解説します.
なかなか予定通りに進めるのは難しい.
講義ノートのミスプリ訂正:p.27,scaler--->scalar,(2.3.7)式の右辺にマイナス.
出席者48名.
2007年11月14日
第6回.
第2回演習レポートの解説,ベクトルとは何か,スカラー積,ベクトル積,ベクトルの微分,単位接線ベクトル
ベクトルの復習を丁寧にやりすぎて,空間曲線のところができなかった.
しかし,回収した演習問題を見ると,記法の混乱が非常に多いのに驚く.
ベクトルとスカラーを等置しない,内積に点を打つなど基本的なことの注意が必要.
出席者44名.
2007年10月31日
第5回.
多変数関数の極大,極小,鞍点,主軸変換による対角化,第2回演習レポート
レポート用の演習問題をやった.
ときどきおかしなグラフを目にする.
今日の講義でやったことは,2回微分が全て零でなければ停留点近傍のグラフは図4.4のタイプのものしかないと言うことである.
等高線は,地図と同じに,代表的な「高度」を書き込んだほうが良い.
来週11/7は学会出張のため休講とします.
出席者48名.
2007年10月24日
第4回.
極座標,関数の近似,多変数のTaylor展開,多変数関数の極大,極小,鞍点
<編集の際誤って消してしまったのでコメント消失!>
出席者46名.前回と同じ数だが7人ほど入れ替わり.
2007年10月17日
第3回.
最大傾斜,接平面,法線ベクトル,合成関数の微分
レポート用の演習問題をやった.
全部できた人はあまりいないと思う.
略解を載せたので必ず最後までやっておくこと.
(昨年と同じ問題なので問題文の日付が古いままです)
出席者46名.急に減ったのが心配
2007年10月11日
第2回.
偏微分の順序の交換,全微分,方向微分系係数,勾配ベクトル.
大体昨年度と同じペース.
2回目であり,講義ノートを配布し多分だけ余裕があり,出席代わりの演習問題ができる.
手間はかかるが,教育的にはよさそう.
講義ノート追加配布者8名.出席者56名.
2007年10月03日
第1回.
講義の進め方についての案内.多変数関数,ベクトル値関数,偏微分の定義,高次の微分.演習(ノートp.9).
この講義のTAは武居佑二氏(R研究室修士1年生),連絡先は ytakesue@r.phys.nagoya-u.ac.jp ,理学部B524または理学館502.
5階のレポートの添削をしてくれます.また,尋ねれば質問にも答えてもらえます.
受講登録が72名,追加申請4名,出席者52名.大体予想通りである.