 へ
へ
2009年1月28日
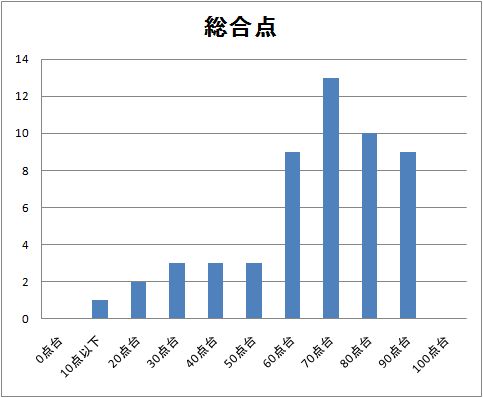
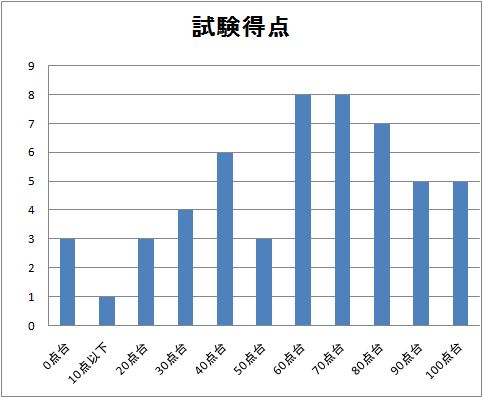
期末試験
出席者53名.
採点はこれからだが解答例を上に載せておきますので復習しておくこと.
2009年1月21日
第13回.
ストクスの定理の意味,ストークスの定理の証明
ストークスの定理の説明と演習.
多変数関数は何を独立変数に取っているかで微分の意味なども変わってくる.
変数を省略して書くことも多いので要注意.
試験前ということもあり,演習問題に関する質問がずいぶん出た.
あと一回補講をやるべきだったかと思う.
演習問題の解答を完全に理解しておくこと.
講義ノートのミスプリを指摘された.
公式集にも入れてあるので重要です.
「おもな公式」の(f)の4番目の式,右辺第2項の符号をマイナスに訂正.
直しておいてください.
今日の演習問題は来週試験の前に返すので,少し早めに来ること.
試験問題は4題出す予定.ガウスの定理とストークスの定理に関連した問題は必ず出します.
出席者45名.
2009年1月14日
第12回.
面積分,ベクトル関数の面積分,ガウスの定理の意味とその証明
予想通り時間がすこし足りない.
最後の2回がこの演習のクライマックスなのだが出席者が少なくなったのが気がかり.
次が最後なので演習問題は2回分配った.
最後だから予習をして,不明な部分は質問してください.
出席者40名.
期末試験は,次々回,1/28(木) 8:45-10:15,いつもと同じ講義室S11です.
ノートなどの持ち込みは不可.
2008年12月25日
第11回.
線積分の意味と定義,ベクトルの線積分,勾配ベクトルの線積分,2重積分,2重積分の順序,積分変数の変換,多重積分とヤコビアン,
積分の話は数学で学んだことの復習が多い.5回分くらいの内容はあるが3回しか講義がないので,できるだけさらっとその意味を復習する.
慣れないと,線積分の意味やベクトルの積分の概念は混乱しやすい.
この講義も教科書も演習問題の数は少ないので,適当な演習書をやってなじむことが大切.
出席者34名.
数日前に講義室変更の知らせがあり,掲示も昨日出されたようなので混乱を心配したが少し早く来て手をうったので無事だった.
クリスマス補講にも関わらず熱心に聞いてくれた諸君に感謝.
今日はこのあとCafe Quante,明日から東京で研究会,年末も結構忙しい.
2008年12月17日
第10回.
2次元極座標でのベクトルの表示,2次限極座標での微分演算子,勾配,発散,ラクラシアン,いくつかの公式の証明.
これでベクトルの微分はおしまい.来週からは積分に入る.
教科書にはこのあたりの話は書いてないので,もう少し勉強したい人はベクトル解析の入門書を探して見てください.
演習問題を見ていると,講義についてこれなくなっているのではないかと疑われる人が数名以上います.
よくあるのだが,ベクトルとスカラーの式を平気で等号で結ぶのはやめてほしい.
時間をかけてしっかり復習することが大事です.
次回は「Xmas Lecture」だが,ケーキは出ません.12月25日(木) 8:45-,S11講義室.
出席者46名.
2008年12月10日
第9回.
レポート問題解説,超流動の渦,ラプラス演算子.
演習問題を丁寧に解説した.具体例は重要なものを挙げてあるので図を描いて,ベクトル場の具体的な感じをつかんでおくとよい.
例によって丁寧に説明すると時間が足りない.極座標までやりたかったのだが....
出席者51名.
2008年12月3日
第8回.
発散の復習,ベクトル場の回転,回転の意味,剛体の回転,レポート演習第3回.
ラプラシアンの説明まで行かなかったが,演習レポートを実施.
4番に書いてある公式の証明はやっておくこと.
とくに一目で分からない複雑なものは計算練習になり理解が深まるので是非やっておいてください.
出席者46名.
数が急に減った.
このあたりから内容が難しくなるので,かなり予習復習をしないとついていけなくなると思う.
それだけにがんばって内容が身につけば,いろいろな物理現象が今まで経験したことのない高い立場から統一的に見えてくるはずだ.
2008年11月26日
第7回.
空間曲線,ベクトル場とは何か,勾配,ベクトル場の発散,流体の流れと発散の意味.
また演習の時間が不足した.全部できた人は1,2名.来週詳しく解説します.
出席者52名.
2008年11月19日
第6回.
第2回演習レポートの解説,ベクトルとは何か,スカラー積,ベクトル積,ベクトルの微分
ベクトルの復習を丁寧にやりすぎて,空間曲線のところができなかった.
集めた演習を見ていると自分勝手な記法が時々ある.
慣用でないもの使用法は勝手に使ってはいけない.
またベクトルとスカラーを等置しないなど基本的なことの注意が必要.
出席者54名.
2008年11月12日
第5回.
主軸変換による対角化,第2回演習レポート
図が白板にうまく書けないので,パソコンを持参して「講義ノート」の図を出して説明した.
設備が良くなって簡単にできる.
無線LANもIDとパスワードさえ調べておけば使えるようだ.
出席者56名.
2007年10月29日
第4回.
関数の近似,多変数のTaylor展開,多変数関数の極大,極小,鞍点
添削したレポートを返却した.
誤って点が付けてあるが,あまり気にしないでよい.やり残したところ,間違ったところは回答を参考に必ず自分でやっておくこと.
今日の演習を見たがかなりグラフには苦労しているようだ.立体図などシュールとしか言えないものもある.
簡潔でわかりやすい図を描くことは変化の様子を理解する鍵になるので訓練しよう.
来週11/05も出張のため休講にします.
補講は12/25の1時間目に決まりました.いつもと同じ講義室S11です.
出席者56名.
2008年10月15日
第3回.
最大傾斜,接平面,法線ベクトル,合成関数の微分
レポート用の演習問題をやった.
全部できた人はあまりいないと思うが,問題(指摘されたミスプリを訂正した)と略解を上に載せておくので必ず最後までやっておくこと.
出席者57名.
毎週3-4名ずつ減っているようだ.
来週10/22と11/05は出張のため休講にします.
クリスマス12/25に補講をするつもりです.
2008年10月08日
第2回.
偏微分の順序の交換,全微分,方向微分系係数,勾配ベクトル.
昨晩,3人の日本人,南部先生,益川先生,小林先生のノーベル物理学賞受賞という嬉しいニュースがあった.
名古屋に関係の深いお二人とのおつきあいはあまりないが,私が学生の頃,京大の助手だった益川さんを覚えている.
ちょうどあのころ同僚の小林さんとノーベル賞になる仕事をされていたということになる.
それから10年近くたって職がなくてフランスにいたころ,F研究室の星野さん,中村さんと,小林さんの4人で車でCote d'Azurを旅したことは楽しい想い出である.
学生諸君にとっても,私にとっても,うれしい「先輩」のノーベル賞だ.
偏微分の微分の順序の表記法について:私が誤って覚えていたようです.fxyは先にxで微分して,次にyで微分するというのが慣用らしい.
ノートなども直しておいてください.
出席者60名.
2008年10月01日
第1回.
講義の進め方についての案内.多変数関数,ベクトル値関数,偏微分の定義,高次の微分.演習(ノートp.9,10).
昨年までは理学部で授業をしたが今年は全学教育棟なので通うのが大変.
こちらでの講義はほとんど10年ぶり.建物もきれいになって気持がよい.
もらった案内図を見ると,昔々私がいた部屋は小さな教室になってしまったようだ.
帰りは図書館に寄って雑誌などを見,思わぬに発見もあった.
往復で20分無駄になるが,週1回くらいは悪くないかもしれない.
(逆に1年生諸君には週1回くらい東のほうに来たほうが良いかもしれないが.)
この講義のTAは梶原和人氏(S研究室修士2年生),連絡先は kajiwara@slab.phys.nagoya-u.ac.jp ,理学館602.
5回のレポートの添削をしてくれます.また,尋ねれば質問にも答えてもらえます.
受講登録が66名(学務情報のページになぜかアクセスできず未だ不明),追加申請8名,出席者64名.大体予想通りである.
追加申請した人は,受講カードを提出しただけでは受講申請にはなりません.
受付期間中に必ずwebから登録してください.