(最終更新 2003/5/22)
研究テーマ: ナノ構造の緩和機構
Research: Relaxation of nanostructures
共同研究者:
一宮彪彦さん,
Ellen Williamsさん,
Ted Einsteinさん,
Phillippe Nozieresさん(Grenoble時代の恩師),
渡邊克博さん(現 日立LSIシステムズ)
もともと結晶の形がステップの運動によってどう決まるかをステップの連続体モデルで調べていた.
特にラフニング転移温度以下でファセットがどのように出現するかに関心がある.
ヘリウムくらいでないと実験はできないと思っていたが,
STMが発明されたおかげで理論が実験と直接比較できるようになってきた.
驚くほど小さなスケールまでステップパラメタによる記述が有効である.
-
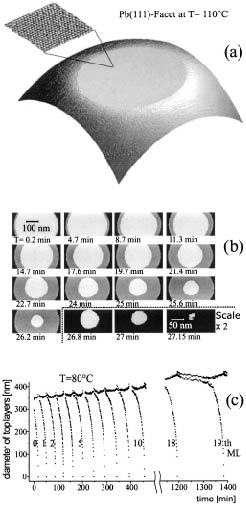
"Step Dynamics in 3D Crystal Shape Relaxation",
K. Thuermer, J. E. Reutt-Robey, E. D. Williams, M. Uwaha, A. Emundts and H. P. Bonzel,
Phys. Rev. Lett. 87 (2001) 186102.
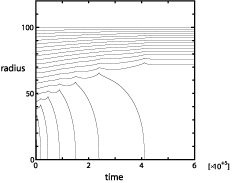
鉛の微結晶のファセット上の原子面が一枚一枚はがれていく様子がじつに美しい(右図,下の図は低温での平衡形に近づいていくときのステップ半径の変化の様子で実験データ(c)に対応するミニチュア版.)
).
-
"Decay of Silicon Mounds: Scaling Laws and Description with Continuum Step Parameters",
A. Ichimiya, K. Hayashi, E. D. Williams, T. L. Einstein, M. Uwaha
and K. Watanabe, Appl. Surf. Sci. 175/176 (2001) 33-35
-
"Decay of Silicon Mounds: Scaling Laws and Description with Continuum Step Parameters",
A. Ichimiya, K. Hayashi, E. D. Williams, T. L. Einstein, M. Uwaha and K. Watanabe, Phys. Rev. Lett. 84 (2000) 3662.
数千個の原子からなるシリコンの3次元的な島の崩壊過程が驚くべきことにステップ・パラメタによってよく記述される.
この実験は一宮研究室(名大工)の研究内容のweb pageで動画が見られる.
-
"Decay of an Island on a Facet via Surface Diffusion",
M. Uwaha and K. Watanabe, J. Phys. Soc. Jpn. 69 (2000) 497.
1988年の論文の発展.
表面拡散による緩和の律則機構とファセット成長の指数との関係を簡単な方法で導いた.
-
"Relaxation of Crystal Shapes Caused by Step Motion",
M. Uwaha, J. Phys. Soc. Jpn. 57 (1988) 1681.
緩和機構とファセットの出現過程の関係を初めて論じた先駆的な仕事.
-
"Crystal Shapes Viewed as Mechanical Equilibrium of Steps",
M. Uwaha and P. Nozieres, in "Morphology and Growth Unit of Crystals" (Proceedings of Oji International Seminar on Morphology and Growth Unit of Crystals, Yamagata, 1985) ed. I. Sunagawa (Terra Scientific Publishing, Tokyo, 1989) pp.17-35.
ステップに働く力がつりあって結晶の平衡形が決まると考えれば,形の変化はステップの運動で記述できる.