 2004年5月20日
2004年5月20日
第6回.ヴィリアル定理のミクロカノニカル・アンサンブルでの証明,カノニカル分布でのヴィリアル定理,ヴィリアル定理の応用--同次関数ポテンシャル,エネルギーの等分配則,調和振動子系の自由エネルギーの計算.
講義でははっきり言わなかったが,ヴィリアルというのは x が座標のときの名称. ヴィリアル定理はクラウジウスによって1870年に導かれた. ただしその証明は力学の長時間平均を使ったものである.
昨年の記録を見るとこの時期にアンケートをとっていた. 来週やることにしよう.
 へ
へ
2004年9月06日
7大戦参加者のための追試験を実施.
80点以上を「優」,55点から75点までを「良」,35点から50点を「可」,30点以下は「不可」として成績を事務に提出した.
優30名,良28名,可15名,不可10名,欠席12名.
採点した答案は事務室で返却します.
2004年7月29日
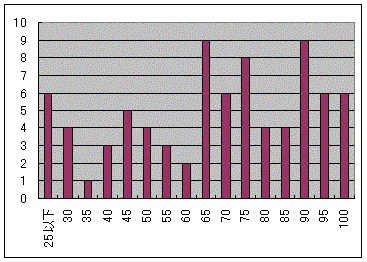
期末試験結果.
5点単位で採点した.
配点は問題に書いたとおり.
3 は何か書いた人は5点(何も書いてない人もいました),とくに有益なコメントには10点.
平均点65点で得点分布はグラフのとおり.
80点以上を「優」,55点から75点までを「良」,35点から50点を「可」,30点以下は「不可」とする予定.
「不可」の者に対しては
2004年度後期中に追試験を行いますので必ず受験してください.
採点した答案は9月になってから事務室で返却します.
3. では,講義で演習問題をやって欲しいという意見が多かった.
講義ノートにも演習問題を入れて欲しいという意見もあった.
検討します.
また同じような試験問題を出すなという声もあった.
比較のためもあって似たものとしたが,やはり問題があるので今後気をつけます.
2004年7月26日
期末試験を実施.
受講登録者95名,受験者80名,申請による欠席3名,欠席12名.
採点が終わったらここに講評を載せる.合格ラインをどうするか,採点してから考えます.
2004年7月15日
第14回.フェルミ分布関数の形,グランドカノニカル分布でのボース粒子,エントロピーを最大にする分布としてのフェルミ分布.
フェルミ分布とボース分布の形と未定なパラメタの決め方について.最後の部分が少し残ったが自習とする.
規定時間数も予定範囲もやってしまったので来週22日は休講.
26日の試験に備えて復習をしっかりやってください.
講義ノートの訂正:
P.48,(26)式,1行目右辺:- b ---> + b
P.49,(30)式,1行目右辺: Ml を削除.
2004年7月8日
第13回.化学平衡の条件,質量作用の法則,量子統計の必要性,同種粒子系の波動関数の対称性,カノニカル分布での分配関数,グランドカノニカル分布でのフェルミ粒子.
化学平衡の話を終え,量子統計の基礎の話に入る.
量子力学IIの講義予定の最初のほうに同種粒子系とあったので復習のつもりだったが,まだやっていないとのことで少し調子が狂う.
講義ノートの訂正:
P.43,(3)式,分母のルートのなか:N ! ---> N ! N1 ! N2 ! ...
P.43,(4)式に続く文章に次の分を追加:Ni ! は 1...N のうち同じ i 番目の状態にある粒子数.
P.43,(4)式に続く文章で: ni ---> Ni
授業後の質問: フェルミ分布を導くとき,すべての状態 i で化学ポテンシャルは共通なのか?
答え: いろいろな1粒子状態の間で粒子数の出入りに対し平衡が成り立っていると考えるので化学ポテンシャルはすべての状態について等しいことが必要.

2004年7月1日
第12回.ファンデルワールスの状態方程式の臨界点,混合理想気体の化学ポテンシャル,浸透圧,希薄な2成分系の相平衡.
高校の化学くらいで勉強した(?)いろいろな関係が統計熱力学の知識を活用すると実に簡単に導ける.
最後の講義ノートを配布.COEの講演会が今日の午後なので是非出席するように勧める.反応は....
レポートでも課せばよかったかな.
講義ノートの訂正:
P.41,(70)式:両式の右辺の c はすべて n にする.
2004年6月24日
第11回.相平衡の条件,単純な物質の相図,クラウジウス・クラペイロンの式,ギブスの相律,ファンデルワールスの状態方程式とマクスウェルの規則.
最後の演習問題とCOE講演会
のチラシを配布.
講義の最後の2-3時間は量子統計の基礎をやることにして準備を始めた.
講義ノートの訂正:
P.39,l.9:P = 3 --> P = 3 または P < 3
P.39,l.10:このとき --> P = 3 のとき
P.39,l.11:P = 3 --> P = 4 または P < 4
P.40,(69)式:左辺第1因子第2項先頭の V を削除.
P.40,(61)式:S2 - S2 --> S2 - S1; 積分の上限と下限を入れ替え.
2004年6月17日
第10回.グランドポテンシャルの微分,熱力学ポテンシャルのルジャンドル変換と分配関数のラプラス変換,グランドカノニカル分布での理想気体,グランドカノニカル分布での粒子数のゆらぎと圧縮率の関係.
これでグランドカノニカルアンサンブルについての基礎的な話は終わり.
次回からは相平衡の話をする予定.
2004年6月10日
第9回.グランドカノニカル分布の説明,大分配関数とグランドポテンシャルの定義,それが熱力学でルジャンドル変換によって定義したものと一致すること.
昨年は7月10日の11回目の講義でおなじところをやった.
今年は余裕余裕.
講義ノートは今日のものが最終なので別な材料を用意しないといけない.
講義ノートの訂正: P.31,(6)式:添え字の N を削除
講義ノートの訂正: P.29,(48)式:右辺全体にかかっている T を削除.
授業後の質問: 常磁性磁気モーメントの時には積分が cosq dq df だったのに,
2原子分子の分配関数の計算では位相空間での積分が dq df dpq dpf になっているのは何故か?
答え: dx dy dz = r2 cosq dr dq df,
dpx dpy dpz = ( r2 cosq )-1 dpr dpq dpf
だから.
 2004年5月27日
2004年5月27日
期末試験の予定: 7月26日(月) 10:30-12:00 B5講義室
 2004年5月20日
2004年5月20日
第6回.ヴィリアル定理のミクロカノニカル・アンサンブルでの証明,カノニカル分布でのヴィリアル定理,ヴィリアル定理の応用--同次関数ポテンシャル,エネルギーの等分配則,調和振動子系の自由エネルギーの計算.
講義でははっきり言わなかったが,ヴィリアルというのは x が座標のときの名称.
ヴィリアル定理はクラウジウスによって1870年に導かれた.
ただしその証明は力学の長時間平均を使ったものである.
昨年の記録を見るとこの時期にアンケートをとっていた.
来週やることにしよう.
講義ノートの訂正: P.22,(81)式の前:f = 2N ---> f = 6N
授業後の質問: 等分配則で式は総和の形になっているが...
答え: 式は総和の形で書いてしまったが,一つ一つの自由度についてエネルギーが kBT/2 になっている.
授業後の質問: 「系の自由度」というときに座標と運動量は別々に数えるのか?
答え: 力学では座標と運動量は必ずセットになって出てくるので一組で1だが,ここではハミルトニアンのなかの一つの項の意味なので別に数えた.
 2004年4月8日
2004年4月8日
第1回.
講義の進め方についての案内. アンサンブルの概念,ミクロカノニカル・アンサンブル,エルゴード仮説,リューヴィル
の定理,定常状態の分布の性質. アンサンブル理論はおもしろいが抽象的でやや難解である.統計力学はいろいろな(ある意味では矛盾する)概念を柔軟に駆使する必要がある.一度には理解しがたいと思うが(本当に理解するのは量子力学と同じように非常に困難!)だんだんに慣れてください.
やはり最初の講義は人数が多い.90の座席がほぼいっぱい.ある程度覚悟していたがこの講義室の使い勝手は非常に悪い.教壇が1/3しかないので背の低い人は黒板の半分しか使えない(しかも黒板が少し小さい).マイクがない.天井むき出しで音響効果も悪いのではないか? 驚いたことに机が全部逆を向いている!(これは授業の前に直してもらったが) とりえは新しいこと,近いこと(誰にとって?),椅子がB5よりはまし.そのうち少しずつ直るでしょう.
講義のときに言ったが統計物理学Iの追試はできれば名大祭のころにやりたい.