(2002/05/20)
授業の感想
少しいろいろな事をしゃべり過ぎた．
消化不良になってしまったのではないかと反省している．
ついてこれなくなった人が多かったのか，後半で居眠りをしていた人が例年に比べ異常に多かった．
これは私の話し方が悪かったせいであることを祈っています．
授業中に回したサンプルのひとつがはじめのほうの安眠者のところで止まってほとんど回らなかったようです．
下に写真が載っていますので見ておいてください．
5月20日 レポートが届きました．
幾何学的選別のスケーリング則については何人かの人が書いていますが，残念ながら満足のいくものはごく僅かしかありませんでした．
下に説明をいれておきます．
講義内容予定
結晶成長の問題が統計物理のなかでどのように位置づけられるかを話し，
統計力学(および連続体力学)を学習する動機づけとし，
同時に結晶成長の物理の面白さと意義を伝える．
-
はじめに [物性理論研究室の紹介 --- 統計力学との関連で]
-
統計物理学は量子力学の基礎に立って多体系の性質を解明する．
-
平衡状態，平衡に近い状態の物性の解明，とくに固体電子論が研究室の中心課題．
-
もうひとつの柱は，非平衡状態の発展法則を探ること．
非平衡系では平衡系のような簡単な原理ひとつではすまない．
秩序化過程の解明を結晶成長を例として研究している．
これは同時に界面，表面の物理学の問題でもある．
-
自然界に見られる多様な結晶の形態
-
(アートギャラリー)(鉱物の写真)(雪と霜)
-
平衡系と成長形が区別される --- 成長形が多様な結晶形態を作り出す．
-
平衡形について(NaCl，MgO，Pbの写真)．
-
平衡形は界面の自由エネルギーを最小にする形．
-
平衡状態の統計力学の問題(ラフニング転移，2次元平衡形)
---原子レベルの相互作用からどのように界面自由エネルギーを求めるか，
表面の相転移についての研究(連続転移，結晶の成長機構と密接に関連)
-
成長形について(秩序化過程のダイナミクスを理解することが必要,
いくつかの実例)
-
メゾスコピックパターン形成
-
観測手段の進歩により原子レベルでの運動が直接，実空間で捉えられるようになった(電子顕微鏡，STM)．
-
島の緩和過程
鉛の島でのファセットの形成過程．
ナノメーターサイズのSi表面での3次元島の崩壊過程がステップパラメタによってよく記述される．
これからステップ間相互作用や緩和機構などについての貴重な情報が得られる．
(この問題については，私の研究テーマ「ナノ構造の緩和機構」参照)
賢島のお土産物屋で買ったメノウのコースターの一部
豊橋の博物館で買ったバイエルン産しのぶ石 
結晶の幾何学的選別
メノウの空洞の周辺部分に良く見られるパターンで，
速く成長する方位の結晶が遅いものを侵食して大きくなる．
直線状に分布した種から成長する2次元結晶の大きさが下地からの距離とともにどのように大きくなるかを考えてみよう．
n 方向への成長速度を v ( n ) とし，それによって決まる成長形がたとえば正方形ならば，角の方向 < 1 1 > が最も成長の早い方向で， < 1 1 > 方向と下地への垂線の角度 q が小さい結晶ほどあとまで生き残る．
初期の形の変化は複雑だが，ある程度成長して隙間がなくなった状態では，q の小さな柱状の分域(domain)が並んで上へ向かって成長する．
それぞれの分域の頂点の横方向へ進行速度は， < 1 1 > 方向の成長速度を v0 とすると v0 sinq である．
水平方向の分域の大きさが L 程度のとき(単位長さあたりの結晶の数を N とすると L=1/N ) これと隣との「衝突」によって片方の成長が阻止されるまでの時間 t ~ L/ v0 Dq である(Dq は生き残っている結晶の傾きの範囲)．
初めにあらゆる方向をランダムに向いていた種のうち生き残っているものの数は Dq に比例し，L ~ 1/N ~ 1/Dq だから，t ~ L2 の関係が得られる．
以上のようにして，下地から h ~ v0 t の高さまで成長したときの分域の大きさ L は t1/2 に比例し，分域の数 N は t- 1/2 に比例するという結論が得られる．
現実の平面を下地とする3次元結晶の場合には N ~ 1/L2 だから N ~ 1/t となる．
これを発見した実験家の要請にこたえて分域の分布についての正確な関係を数学的に導いたのは確率論で有名な数学者のKolmogorovであった．
自然界に見られる一群のパターンを特徴づける概念である．
「ある図形のどの一部を拡大または縮小してももとの図形と同じように見える」ものをフラクタル(fractal)図形と呼ぶ．
自然界のものでは冬枯れの樹木などがこのパターンに近い．
小枝を拡大したものが大きな枝のパターンと似ているからである．
フラクタル図形は穴だらけでスカスカである．
何故なら，穴がひとつあるとすれば，それを拡大縮小したあらゆる大きさの穴がいたるところになければならないからである．
これに対してびっしり詰まっているか，あるいは大きな穴のないふつうの図形をコンパクト(compact)図形と呼ぶ．
コンパクトな図形では体積 V は差渡しの長さ L の3乗に比例し，面積は L の2乗に比例する．
この3や2という数はその図形の埋めこまれている空間の次元数である．
フラクタルではフラクタル次元(fractal dimension)と呼ばれる指数 Df が空間の次元数 d よりも小さい．
つまり図形の大きさ(1次元的な広がり)とその中に含まれるフラクタル図形の体積や面積，あるいは現実のものなら物質量 M，のあいだの関係が M~ LDf となり，Df < d である．
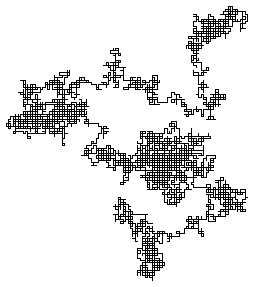
フラクタルパターンの最も簡単な例として，正方格子上のランダムウォークの図をのせておく．それぞれ，100歩，1000歩，10000歩，100000歩，1000000歩の軌跡である(田崎晴明さんのプログラムで画いた)．
注目すべきことは，1)みんなパターンの感じが似ている，2)全体の大きさは歩数の平方根に比例，3)小さいものは大きいものの一部である．
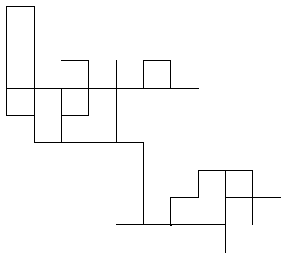
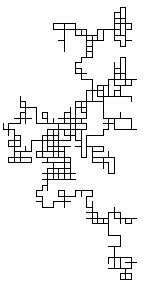
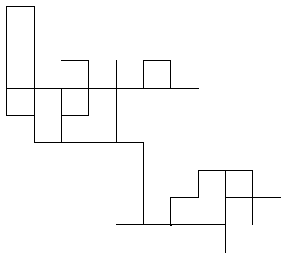
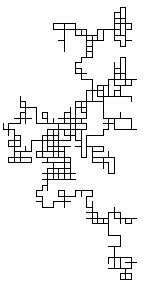
(フラクタルについて詳しく知りたいひとは，東北大の早川美徳さんが「フラクタル入門」をWEBに載せているので見てください．)